How Many Powerball Tickets Should I Buy?
It’s not completely stupid. The Powerball jackpot currently stands at $1.5 billion, with a $930 million cash value. There are only 292 million possible combinations of numbers, so there exists an arbitratrage opportunity where one could buy up every possible number combination and walk away with $346 million.
But just because tickets have a positive expected value doesn’t mean I should buy as many as I can afford. There comes a point at which the 100% chance of going broke outweighs the fractional chance of winning $1.5 billion dollars.
The correct answer is to identify the point where the expected value of my gains approximately equal the negative utility of my loss.
Disutility
My unhappiness isn’t a linearly increasing function with each dollar I lose. I certainly wouldn’t miss the first few. In fact, I might become happier spending a few dollars, because I’m buying hope.
Later, when I’m losing massive amounts of money, my disutility accelerates. It’s asymptotic, because beyond a certain point I’ll probably just jump off a bridge.
Calibration
At about $100, I start feeling pain. At $1000, I’m really quite bummed. At $80,000, I’m ready to kill myself. Not because I’m broke, but rather for the greater good of the gene pool because I just spent a years’ salary on freaking lottery tickets.
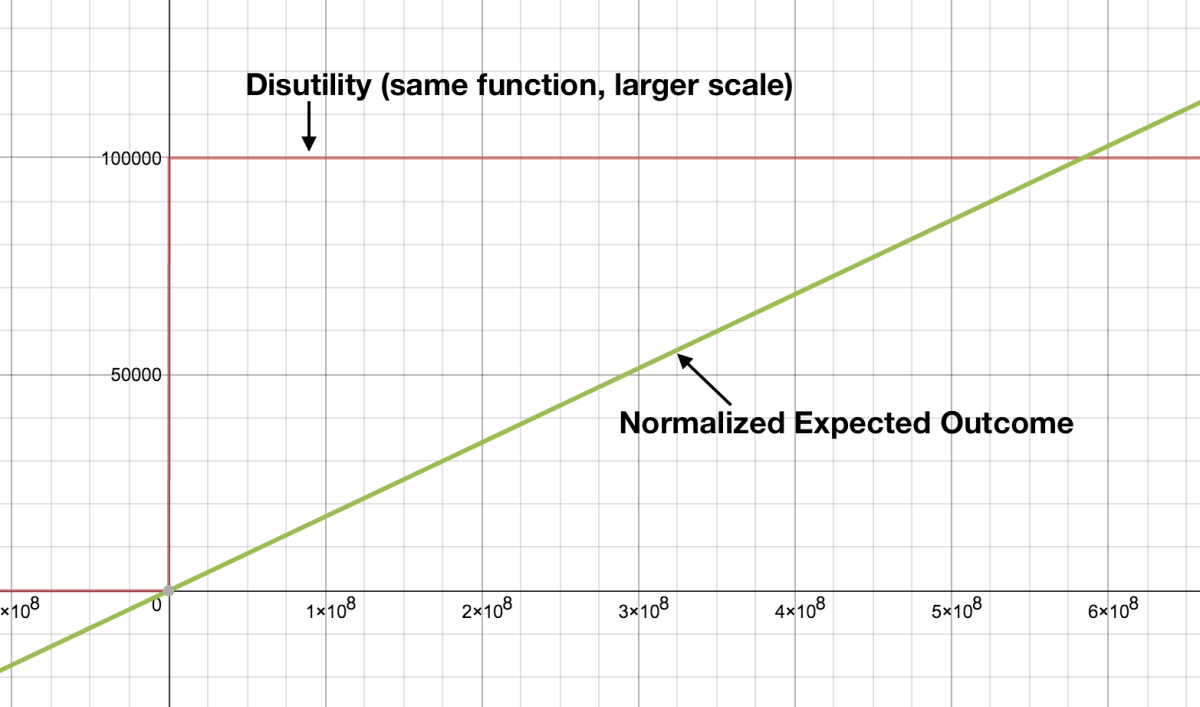
Now, the expectation of winning the Powerball is a linear function as each ticket increases my chances. We can normalize this to the disutility function by assuming my maximum positive utility is equal to the maximum disutility.
I’m going to ignore proration risk here: It’s fine if I have to share the jackpot with one or more other winners. My happiness maxes out long before $1.5 billion. Even before $100 million. I’ve done a lot of drugs, I know where my limits are.
So we find the point where my disutility first exceeds the expected positive outcome:

400. I should buy 400 tickets.
Although if I wanted to maximize the positive delta between expected outcome and disutility, I should only buy one. In reality, I’m lazy so I’ll end up buying zer0.